Teorema do valor médio
Postado em 2024-05-09 17:35:10
atualizado em 2024-05-11 08:02:17
Introdução
O Teorema do Valor Médio é um conceito aprendido no cálculo diferencial, área que estuda as taxas de variação de grandezas. Ele descreve uma propriedade importante das funções contínuas em um intervalo específico e tem aplicações significativas em diversas áreas, desde a física até a economia.
Imagine-se dirigindo em uma estrada sinuosa. Você sabe que em algum momento, sua velocidade média durante o percurso será igual à velocidade instantânea em algum ponto. Este é um exemplo simplificado do que o Teorema do Valor Médio descreve matematicamente para funções contínuas em um intervalo fechado.
Basicamente, este teorema estabelece que, se uma função \(f(x)\) é contínua em um intervalo fechado \([a,b]\) e diferenciável em um intervalo aberto \((a,b)\), então existe pelo menos um ponto \(c\) dentro desse intervalo aberto onde a taxa média de variação da função é igual à sua taxa de variação instantânea em \(c\).
Matematicamente, o Teorema do Valor Médio pode ser formulado da seguinte maneira:
Se \(f(x)\) é contínua em \([a,b]\) e diferenciável em \((a,b)\), então existe pelo menos um número \(c\) em \((a,b)\) tal que:
\(f'(c) = \frac{f(b) - f(a)}{b - a}\)
Onde:
\(f’(c)\) é a taxa de variação instantânea da função em \(c\) (derivada de \(f(x)\) em \(c\));
a taxa média de variação da função no intervalo \([a,b]\).
Em termos mais simples, o teorema afirma que em algum ponto dentro do intervalo aberto, a taxa de variação instantânea da função (a inclinação da reta tangente \(t\) à curva) é igual à inclinação média da reta secante que une os pontos \((a,f(a))\) e \((b,f(b))\) no gráfico da função.
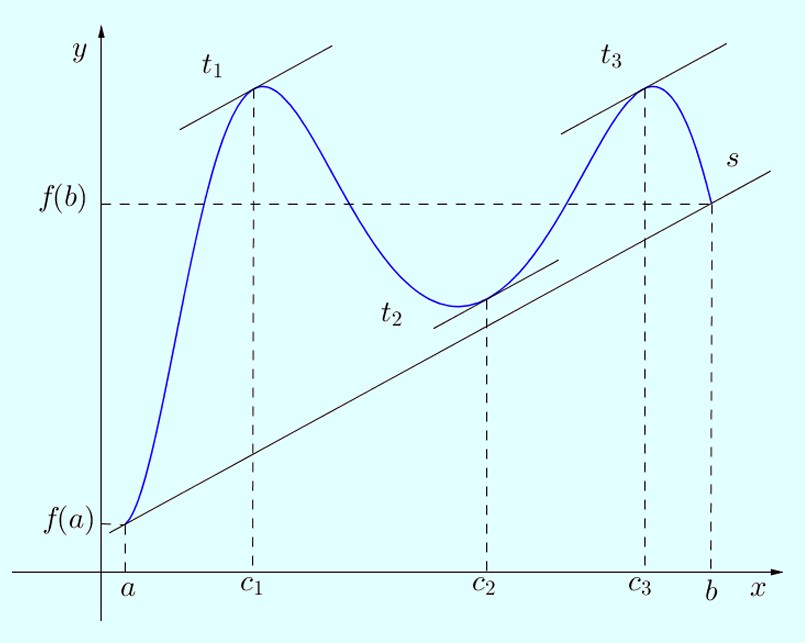
Ilustração
Exemplo
Determine os valores \(c ∈ (a,b)\) tais que \(f'(c) = \frac{f(b) - f(a)}{b - a}\) em que \(f(x) = -\frac{1}{x^2}, \quad a = -3 \quad\) e \(\quad b = -1\).
Resolução
Note que,
\(f(x) = -x^{-2}\)
Portanto,
\(f'(x) = 2x^{-3}\)
e que,
\(f(-3) = -\frac{1}{(-3)^2} = -\frac{1}{9}\)
\(f(-1) = -\frac{1}{(-1)^2} = -1\)
Então,
\(f'(c) = \frac{f(-1) - f(-3)}{-1 - (-3)}\)
\(2c^{-3} = \frac{-1 - (-\frac{1}{9})}{2}\)
\(4 = -\frac{8}{9} c^{3}\)
\(-\frac{36}{8} = c^{3}\)
\(\sqrt[3]{-\frac{9}{2}} = c\)
Logo, \(\sqrt[3]{-\frac{9}{2}} ∈ (-3,-1)\).
by cimurro